CHAPTER 3 - ચતુષ્કોણ ની સમજ

 સ્વાધ્યાય 3.1 

પ્રશ્ન 1. અહીં કેટલીક આકૃતિઓ આપેલ છે.

પ્રત્યેકનું નીચે દર્શાવેલ આધાર પ્રમાણે વર્ગીકરણ કરો:
(a) સરળ વક્ર
(b) સરળ બંધ વક્ર
(c) બહુકોણ
(d) બહિર્મુખ બહુકોણ
(e) અંતર્મુખ બહુકોણ

ઉત્તર :-
(a) સરળ વક્રઃ (1), (2), (5), (6) અને (7)
(b) સરળ બંધ વક્ર : ( 1), (2), (5), (6) અને (7)
(c) બહુકોણ : (1), (2) અને (4)
(d) બહિર્મુખ બહુકોણ : (2)
(e) અંતર્મુખ બહુકોણ (1) અને (4)

પ્રશ્ન 2. નીચે દર્શાવેલ પ્રત્યેકને કેટલા વિકર્ણ છે તે જણાવો:
(a) બહિર્મુખ ચતુષ્કોણ
(b) નિયમિત ષટ્કોણ
(c) ત્રિકોણ

ઉત્તર :-
સૂત્ર યાદ રાખોઃ
n બાજુઓવાળા બહુકોણના વિકર્ણોની સંખ્યા
= [n(n−1)2−n]
= n2−n−2n2
= n2−3n2
(a) બહિર્મુખ ચતુષ્કોણને ચાર બાજુઓ હોય છે. ∴ n = 4
∴ વિકણની સંખ્યા = [4(4−1)2−4]
= [4(3)2−4]
= [122−4]
= [6 – 4]
= 2

(b) નિયમિત પકોણને છ બાજુઓ હોય છે. ∴ n = 6
∴ વિકર્ણોની સંખ્યા = [6(6−1)2−6]
= [6(5)2−6]
= [302−6]
= [15 – 6]
= 9

(c) ત્રિકોણને ત્રણ બાજુઓ હોય છે. ∴ n = 3
∴ વિકર્ણોની સંખ્યા = [3(3−1)2−3]
= [3(2)2−3]
= [62−3]
= [3 – 3]
= 0

પ્રશ્ન 3. બહિર્મુખ ચતુષ્કોણના ખૂણાનાં માપનો સરવાળો કેટલો થાય? હવે જો, ચતુષ્કોણ બહિર્મુખ ના હોય, તો શું આ ગુણધર્મ લાગુ પડશે? (એક બહિર્મુખ ના હોય તેવો ચતુષ્કોણ બનાવો અને પ્રયત્ન કરો.)

ઉત્તર :-

બહિર્મુખ ચતુષ્કોણના બધા ખૂણાનાં માપનો સરવાળો 360° થાય છે.
જો ચતુષ્કોણ બહિર્મુખ ના હોય, એટલે કે અંતર્મુખ હોય તોપણ હા, તેના બધા ખૂણાનાં માપનો સરવાળો 360° થાય છે.
જુઓ અહીં ▢ ABCD અંતર્મુખ ચતુષ્કોણ છે.

તેમાં m∠A + m∠B + m∠C + m∠D
= 40° + 55° + 35° + 230° = 360°

પ્રશ્ન 4. નીચેનું કોષ્ટક જુઓ. (અહીં પ્રત્યેક આકૃતિને ત્રિકોણમાં વિભાજિત કરેલ છે અને તેના પરથી ખૂણાનાં માપનો સરવાળો શોધેલ છે.)

નિમ્નલિખિત સંખ્યા દર્શાવતી બાજુઓ ધરાવતા બહુકોણના ખૂણાનાં માપના સરવાળા વિશે શું કહી શકાય?
(a) 7
(5) 8
(c) 10
(d) n

ઉત્તરઃ

ઉપરના કોષ્ટક પરથી અનુમાન કરી શકાય કે n-બાજુઓ ધરાવતા બહુકોણના અંદરના બધા ખૂણાનાં માપનો સરવાળો = (n – 2) × 180°
(a) 7 બાજુઓવાળા બહુકોણ માટે અહીં, n = 7 લઈશું:
= (n – 2) × 180°
અંદરના બધા ખૂણાઓનાં માપનો સરવાળો = (7 – 2) × 180°
= 5 × 180° = 900°

(b) 8 બાજુઓવાળા બહુકોણ માટે અહીં, n = 8
લઈશું: અંદરના બધા ખૂણાઓનાં માપનો સરવાળો = (n – 2) × 180°
= (8 – 20) × 180° = 6 × 180° = 1080°

(c) 10 બાજુઓવાળા બહુકોણ માટે : અહીં, n = 10 લઈશું :
અંદરના બધા ખૂણાઓનાં માપનો સરવાળો = (n – 2) × 180°
= (10 – 2) × 180° = 8 × 180° = 1440°

(d) n બાજુઓવાળા બહુકોણ માટે:
અંદરના બધા ખૂણાઓનાં માપનો સરવાળો = (n – 2) × 180°

પ્રશ્ન 5. નિયમિત બહુકોણ એટલે શું? એવા નિયમિત બહુકોણનાં નામ આપો જેમાં:
(i) 3 બાજુ હોય
(ii) 4 બાજુ હોય
(iii) 6 બાજુ હોય

ઉત્તરઃ

નિયમિત બહુકોણ એટલે –
(1) અંદરના બધા જ ખૂણાઓનાં માપ સરખાં હોય
(2) બહુકોણની બધી જ બાજુઓનાં માપ સરખાં હોય
માગેલા બહુકોણનાં નામ:
(i) 3 બાજુ હોયઃ સમબાજુ ત્રિકોણ
(ii) 4 બાજુ હોયઃ ચોરસ
(iii) 6 બાજુ હોયઃ નિયમિત પકોણ

પ્રશ્ન 6. નીચેની આકૃતિઓમાં x (ખૂણાનું માપ) શોધો :

(a) 

ઉત્તરઃ
ચતુષ્કોણના ચારેય ખૂણાઓનાં માપનો સરવાળો = 360°
∴ x + 120° + 130° + 50° = 360°
∴ x + 300° = 360°
∴ x = 360° – 300° (∵ 300° ને જ.બા. લઈ જતાં)
∴ x = 60°

(b)

ઉત્તરઃ
ચતુષ્કોણના ચારેય ખૂણાઓનાં માપનો સરવાળો = 360°
∴ x + 60° + 70° + 90° = 360°
∴ x + 220° = 360°
∴ x = 360° – 220° (∵ 220° ને જ.બા. લઈ જતાં)
∴ x = 140°

(c)

ઉત્તરઃ
અહીં ચતુષ્કોણના પાયાના બે ખૂણાઓ રેખિક જોડના ખૂણા બનાવે છે.
∴ પાયાના બે ખૂણાનાં માપ અનુક્રમે (180° – 70°) = 110° અને (180° – 60°) = 120° છે.
અહીં આપેલી આકૃતિ પંચકોણની છે.
∴ પંચકોણના અંદરના બધા ખૂણાઓનાં માપનો સરવાળો
= (n – 2) × 180 = (5 – 2) × 180 = 3 × 180 = 540
∴ 30° + x + x + 110° + 120° = 540°
∴ 2x + 260° = 540°
∴ 2x = 540° – 260° (∵260°ને જ.બા. લઈ જતાં)
∴ 2x = 280°
∴ 2x2=280∘2 (∵ બંને બાજુ 2 વડે ભાગતા)
∴ x = 140°

(d)

ઉત્તરઃ
અહીં આપેલી આકૃતિ એ નિયમિત પંચકોણની છે.
નિયમિત પંચકોણના અંદરના બધા ખૂણાઓનાં માપ સરખાં હોય છે.
ધારો કે, આ દરેક ખૂણાનું માપ x છે.
નિયમિત પંચકોણના અંદરના બધા ખૂણાઓનાં માપનો સરવાળો
(5 – 2) × 180 = 3 × 180° = 540°
∴ x + x + x + x + x = 540°
∴ 5x = 540°
∴ 5x5=540∘5 (∵ બંને બાજુ 5 વડે ભાગતાં)
∴ x = 108°

પ્રશ્ન 7. (a) x + y + z શોધો.

ઉત્તરઃ
x + 90° = 180° (∵ રૈખિક જોડના ખૂણા)
∴ x = 180° – 90° ∴ x = 90°
y = 30° + 90° (∵ અંતઃસંમુખકોણનો સરવાળો)
∴ y = 120°
z = 180° – 30° (∵ રેખિક જોડના ખૂણા)
∴ z = 150°
હવે, x + y + z = 90° + 120° + 150° = 360°

(b) x + y + z + w શોધો.

ઉત્તરઃ
સૌપ્રથમ વ ખૂણાનું માપ શોધવું પડશે.
ચતુષ્કોણના અંદરના બધા ખૂણાઓનાં માપનો સરવાળો = 360°

∴ a + 120° + 80° + 60° = 360°
∴ a + 260° = 360°
∴ a = 360° – 260° ∴ a = 100°
હવે, x + 120° = 180°
(∵ રેખિક જોડના ખૂણા)
∴ x = 180° – 120° ∴ x = 60°
વળી, y + 80° = 180°
(∵ રેખિક જોડના ખૂણા)
∴ y = 180° – 80° ∴ y = 100°
વળી, z + 60° = 180° (∵ રેખિક જોડના ખૂણા)
∴ z = 180° – 60° ∴ z = 120°
વળી, w + 100° = 180° (∵ રેખિક જોડના ખૂણા)
∴ w = 180° – 100° ∴ w = 80°
આમ, x + y + z + w = 60° + 100° + 120° + 80° = 360°

 સ્વાધ્યાય 3.2 

પ્રશ્ન 1. નીચેની આકૃતિઓમાં x શોધોઃ
(a) 

ઉત્તરઃ
આ આકૃતિ માટે આકૃતિના બધા બહિષ્કોણનાં માપનો સરવાળો = 360°
∴ x + 125° + 125° = 360°
∴ x + 250° = 360°
∴ x = 360° – 250° (∵ 250°ને જ.બા. લઈ જતાં)
∴ x = 110°

(b)

ઉત્તરઃ
આ આકૃતિમાં એક બહિષ્કોણ 90° છે અને બીજો અંત:કોણ 90° છે.
∴ આકૃતિમાં બે બહિષ્કોણ 90ના છે.
આ આકૃતિના બધા બહિષ્કોણનાં માપનો સરવાળો = 360°
∴ x + 90° + 60° + 90° + 70° = 360°
∴ x + 310° = 360°
∴ x = 360° – 310° (∵ 310ને જ.બા. લઈ જતાં)
∴ x = 50°

પ્રશ્ન 2. નીચે પ્રમાણેની બાજુઓ ધરાવતા નિયમિત બહુકોણમાં બહિષ્કોણનું માપ શોધોઃ

(a) 9 બાજુ

9 બાજુવાળા :
અહીં બહુકોણને 9 બાજુઓ છે. તેથી n = 9 લઈશું.
9 બાજુવાળા બહુકોણના બહિષ્કોણની સંખ્યા 9 હોય.
આ નિયમિત બહુકોણ છે. તેથી તેના દરેક બહિષ્કોણનું માપ સરખું હોય.
હવે, બહુકોણના બધા બહિષ્કોણનાં માપનો સરવાળો 360° થાય છે.
∴ 9 બાજુવાળા બહુકોણના દરેક બહિષ્કોણનું માપ
= 360∘n=360∘9 = 40°

(b) 15 બાજુ


15 બાજુવાળા :
અહીં બહુકોણને 15 બાજુઓ છે. તેથી n = 15 લઈશું.
15 બાજુવાળા બહુકોણના બહિષ્કોણની સંખ્યા 15 હોય.
આ નિયમિત બહુકોણ છે. તેથી તેના દરેક બહિષ્કોણનું માપ સરખું હોય.
હવે, બહુકોણના બધા બહિષ્કોણનાં માપનો સરવાળો 360° થાય છે.
∴ 15 બાજુવાળા બહુકોણનાં દરેક બહિષ્કોણનું માપ
= 360∘n=360∘15 = 24°

પ્રશ્ન 3. એક નિયમિત બહુકોણને કેટલી બાજુઓ હોય તો તેના દરેક બહિષ્કોણનું માપ 24° થાય?
ઉત્તરઃ

અહીં, બહુકોણ નિયમિત છે. તેથી તેના દરેક બહિષ્કોણનું માપ સરખું હોય.
બહુકોણના બધા બહિષ્કોણનાં માપનો સરવાળો 360° થાય છે.
હવે, આ બહુકોણના બહિષ્કોણનું માપ 24° છે.
∴ આ બહુકોણના ખૂણાઓની સંખ્યા = 360∘24∘ = 15
આ નિયમિત બહુકોણને જેટલા ખૂણા તેટલી બાજુઓ હોય.
∴ આ બહુકોણને કુલ 15 બાજુઓ છે.

પ્રશ્ન 4. એક નિયમિત બહુકોણને કેટલી બાજુઓ હોય તો તેના દરેક અંતઃકોણનું માપ 165° થાય?


બહુકોણ નિયમિત છે અને તેના દરેક અંતઃકોણનું માપ 165° છે.
∴ બહુકોણના દરેક બહિષ્કોણનું માપ = 180° – 165° = 15
બહુકોણના બધા બહિષ્કોણનાં માપનો સરવાળો 360° થાય છે.
∴ બહુકોણની બાજુઓની સંખ્યા = 360∘15∘ = 24
આ બહુકોણને કુલ 24 બાજુઓ છે.

પ્રશ્ન 5. (a) એવો નિયમિત બહુકોણ શક્ય છે કે જેમાં દરેક બહિષ્કોણનું માપ 22° હોય?
ઉત્તરઃ
આ બહુકોણના બહિષ્કોણનું માપ 22° છે.
∴ બહુકોણની બાજુઓની સંખ્યા = 360∘22∘ = 18011
જો આ બહુકોણ એ નિયમિત બહુકોણ હોય, તો તેની બાજુઓની સંખ્યા એ પૂર્ણ અંકમાં મળે.
જુઓ 180∘11 એ પૂર્ણ સંખ્યા નથી.
∴ ના, નિયમિત બહુકોણ બહિષ્કોણનું માપ 22° ન હોઈ શકે.

(b) શું આ માપ નિયમિત બહુકોણના અંતઃકોણનું હોઈ શકે? કેમ?
ઉત્તરઃ
આ બહુકોણના અંદરના ખૂણાનું માપ 22° છે.
∴ બહુકોણના બહિષ્કોણનું માપ = 180° – 22° = 158° થાય.
∴ બહુકોણની બાજુઓની સંખ્યા = 360∘158∘=18079
જો બહુકોણ એ નિયમિત બહુકોણ હોય, તો તેની બાજુઓની સંખ્યા એ પૂર્ણ અંકમાં મળે.
જુઓ 18079 એ પૂર્ણ સંખ્યા નથી.
∴ ના, નિયમિત બહુકોણના અંતઃકોણનું માપ 22° ન હોઈ શકે.

પ્રશ્ન 6.
(a) નિયમિત બહુકોણમાં અંતઃકોણનું ઓછામાં ઓછું માપ કેટલું હોઈ શકે? કેમ?
ઉત્તરઃ
નિયમિત બહુકોણની બાજુઓની સંખ્યા ઓછામાં ઓછી 3 હોય.
∴ 3 બાજુઓવાળો નિયમિત બહુકોણ એ સમબાજુ ત્રિકોણ છે.
સમબાજુ ત્રિકોણના દરેક ખૂણાનું માપ 60° છે.
∴ નિયમિત બહુકોણના પ્રત્યેક અંતઃકોણનું માપ ઓછામાં ઓછું 60° હોઈ શકે.

(b) નિયમિત બહુકોણમાં બહિષ્કોણનું વધુમાં વધુ માપ કેટલું હોઈ શકે?
ઉત્તરઃ
નિયમિત બહુકોણના પ્રત્યેક અંતઃકોણનું માપ + તેના બહિષ્કોણનું માપ = 180°
હવે નિયમિત બહુકોણના પ્રત્યેક અંતઃકોણનું ઓછામાં ઓછું માપ = 60°
∴ બહુકોણના બહિષ્કોણનું માપ વધુમાં વધુ 180° – 60° = 120° હોય.

સ્વાધ્યાય 3.3

પ્રશ્ન 1. સમાંતરબાજુ ચતુષ્કોણ ABCD આપેલ છે. દરેક વિધાનને તેમાં ઉપયોગ કરવામાં આવેલ વ્યાખ્યા અથવા ગુણધર્મનો ઉપયોગ કરીને પૂરું કરો:

(i) AD = ………….
(ii) ZDCB = …………..
(iii) OC = ……………..
(iv) m∠DAB + m∠CDA = ……………

ઉત્તરઃ
(i) AD = BC
કારણ: સમાંતરબાજુ ચતુષ્કોણની સામસામેની બાજુઓની લંબાઈ સરખી હોય છે.

(ii) ∠DCB = ∠DAB
કારણ: સમાંતરબાજુ ચતુષ્કોણના સામસામેના ખૂણાનાં માપ સરખાં હોય છે.

(iii) OC = OA
કારણઃ સમાંતરબાજુ ચતુષ્કોણના વિકણે પરસ્પર દુભાગે છે.

(iv) m∠DAB + m∠CDA = 180°
કારણ: સમાંતરબાજુ ચતુષ્કોણમાં પાસપાસેના બે ખૂણાઓ પૂરક હોય છે.

પ્રશ્ન 2. નીચેના સમાંતરબાજુ ચતુષ્કોણમાં x, y અને zનાં મૂલ્ય શોધોઃ
(i)

ઉત્તરઃ
□ ABCD સમાંતરબાજુ ચતુષ્કોણ છે.

∴ ∠B = ∠D ∴ y = 100° (∵ સામસામેના ખૂણા)
હવે, y + z = 180° (∵ પાસપાસેના ખૂણા પૂરક હોય છે.)
∴ 100 + z = 180°
∴ z = 180° – 100°
∴ z = 80°
હવે, x = z (∵ સામસામેના ખૂણા)
∴ x = 80°
આમ, x = 80°, y = 100° અને z = 80°

(ii)

ઉત્તરઃ
આપેલ ચતુષ્કોણ સમાંતરબાજુ ચતુષ્કોણ છે.
∴ m∠P + m∠S = 180° (∵ પાસપાસેના ખૂણા પૂરક હોય છે.)
∴ x + 50° = 180°
∴ x = 180° – 50°
∴ x = 130°

વળી, x = y (∵ સામસામેના ખૂણા)
∴ y = 130°
હવે m∠Q = 50° (∵ ∠S અને ∠Q સામસામેના ખૂણા)
m∠Q + z = 180° (∵ રેખિક જોડના ખૂણા)
∴ 50° + 3 = 180°
∴ z = 180° – 50°
∴ z = 130°
આમ, x = 130°, U = 130° અને z = 130°

(iii)

ઉત્તરઃ
□ ABCD સમાંતરબાજુ ચતુષ્કોણ છે.
તેમાં ∠AMD કાટખૂણો છે.
∴ m∠BMC = 90° અને
∴ m∠AMD = 90° (અભિકોણો)
x = m∠BMC = 90°

Δ BMCના ત્રણે ખૂણાઓનાં માપનો સરવાળો 180° થાય.
∴ y + 90° + 30° = 180°
∴ y + 120° = 180°
∴ y = 180° – 120°
∴ y = 60°
□ ABCDમાં BC¯¯¯¯¯¯¯∥AD¯¯¯¯¯¯¯¯ અને તેમની છેદિકા BD¯¯¯¯¯¯¯ છે.
∴ y = z (∵ યુગ્મકોણો)
∴ z = 60° (∵ y = 60°)
આમ, x = 90°, y = 60° અને z = 60°

(iv)

ઉત્તરઃ
□ ABCD સમાંતરબાજુ ચતુષ્કોણ છે.
∠D = ∠B (∵ સામસામેના ખૂણા)
∴ y = 80°

m∠A + m∠D = 180° (∵ પાસપાસેના પૂરક હોય છે.)
∴ x + y = 180°
∴ x + 80° = 180°
∴ x = 180° – 80°
∴ x = 100°
m∠A = m∠BCD (∵ સામસામેના પૂરક હોય છે.)
∴ 100° = m∠BCD
હવે, z + m∠BCD = 180° (∵ રૈખિક જોડના ખૂણા)
∴ z + 100° = 180°
∴ z = 180° – 100°
∴ z = 80°
આમ, x = 100, y = 80° અને z = 80°

(v)

ઉત્તરઃ
□ ABCD સમાંતરબાજુ ચતુષ્કોણ છે.
∴ m∠B = m∠D (∵ સામસામેના ખૂણા)
∴ y = 112°

m∠A + m∠B = 180° (∵ પાસપાસેના ખૂણા પૂરક હોય છે.)
∴ (40° + z) + 112° = 180°
∴ 40° + z + 112° = 180°
∴ z + 152° = 180°
∴ z = 180° – 152°
∴ z = 28°
હવે, DC¯¯¯¯¯¯¯∥AB¯¯¯¯¯¯¯ અને AC←→ તેમની છેદિકા છે.
∴ z = x
∴ x = 28° (∵ z = 28°)
આમ, x = 28°, y = 112° અને z = 28°

પ્રશ્ન 3.
શું ચતુષ્કોણ ABCD, સમાંતરબાજુ ચતુષ્કોણ થઈ શકે, જો ……………..
(i) ∠D + ∠B = 180°?
(ii) AB = DC = 8 સેમી, AD = 4 સેમી અને BC = 4.4 સેમી?
(iii) ∠A = 70° અને ∠C = 65°?
ઉત્તરઃ
(i) ના, અહીં ∠D અને ∠B એ પાસપાસેના બે ખૂણા નથી.
તેથી ચતુષ્કોણ ABCD સમાંતરબાજુ ચતુષ્કોણ ન થઈ શકે.

(ii) ના, અહીં AD ≠ BC (∵ AD = 4 સેમી અને BC = 4.4 સેમી)
તેથી ચતુષ્કોણ ABCD સમાંતરબાજુ ચતુષ્કોણ ન થઈ શકે.

(iii) ના, m∠A ≠ m∠C (∵ M∠A = 70° અને m∠C = 65°)
તેથી, ચતુષ્કોણ ABCD સમાંતરબાજુ ચતુષ્કોણ ન થઈ શકે.

પ્રશ્ન 4.
એક એવા ચતુષ્કોણની કાચી (Rough) આકૃતિ દોરો કે જે સમાંતરબાજુ ચતુષ્કોણ ના હોય પરંતુ સામસામેના ખૂણાની એક જોડી સમાન હોય.
ઉત્તરઃ

અહીં ચતુષ્કોણ ABCD  છે.
આકૃતિમાં જુઓ.
∠B = ∠D છે.
છતાં □ ABCD એ સમાંતરબાજુ ચતુષ્કોણ નથી.

પ્રશ્ન 5. સમાંતરબાજુ ચતુષ્કોણમાં બે પાસપાસેના ખૂણાનાં માપનો ગુણોત્તર 3 : 2 છે, તો ચતુષ્કોણના બધા જ ખૂણાનાં માપ શોધો.
ઉત્તરઃ
ધારો કે, □ ABCDમાં ∠A અને ∠Bનું માપનું પ્રમાણ 3 : 2 છે.

∴ ∠A એ 3x છે, તો ∠B એ 2x છે.
હવે, m∠A + m∠B = 180° (∵ પાસપાસેના બે ખૂણા પૂરક હોય છે.)
∴ 3x + 2x = 180°
∴ 5x = 180°
∴ x = 180∘5
∴ x = 36°
m∠A = 3x = 3 × 36° = 108° અને
m∠B = 2x = 2 × 36° = 72°
હવે, m∠A = m∠C અને m∠B = m∠D (∵ સામસામેના ખૂણા)
∴ m∠C = 108° અને m∠D = 72°
આમ, □ ABCDમાં ∠A = 108°, ∠B = 72°, ∠C = 108° અને ∠D = 72°

પ્રશ્ન 6. એક સમાંતરબાજુ ચતુષ્કોણના પાસપાસેના ખૂણાની એક જોડના ખૂણાનાં માપ સમાન છે, તો ચતુષ્કોણના બધા જ ખૂણાનાં માપ શોધો.
ઉત્તરઃ
□ ABCD એવો સમાંતરબાજુ ચતુષ્કોણ છે. જેના પાસપાસેના બે ખૂણા ∠A અને ∠B એકરૂપ છે.
∴ ∠A = ∠B
હવે, m∠A + m∠B = 180° (∵ પાસપાસેના બે ખૂણા પૂરક હોય છે.)

∴ m∠A + m∠A = 180° ( m∠B = m∠A)
∴ 2m∠A = 180°
∴ m∠A = 180° = 90°
∴ m∠B = 90°
હવે, m∠A = m∠C અને m∠B = m∠D (∵ સામસામેના ખૂણા)
∴ m∠C = 90° અને m∠D = 90°
આમ, ∠A = 90°, ∠B = 90°, ∠C = 90° અને ∠D = 90° આ ચતુષ્કોણ લંબચોરસ છે.

પ્રશ્ન 7. આકૃતિમાં એક સમાંતરબાજુ ચતુષ્કોણ HOPE દર્શાવેલ છે. x, y, z ખૂણાનાં માપ શોધો. ખૂણો શોધવા કયા ગુણધર્મનો ઉપયોગ કર્યો છે તે જણાવો.

ઉત્તરઃ

ઉત્તરઃ

ΔHOPનો બહિષ્કોણ ∠POA છે.
∴ y + z = 70°
વળી, m∠HOP = 180° – 70° (∵ રેખિક જોડના ખૂણા) ← ગુણધર્મ
∴ m∠HOP = 110°
x = ∠HOP = ∠HEP (∵ સામસામેના ખૂણા) ← ગુણધર્મ
∴ x = 110°
∴ PO¯¯¯¯¯¯¯∥EH¯¯¯¯¯¯¯ ની PH←→ છેદિકા છે.
∴ ∠OPH = ∠FHE (∵ યુગ્મકોણ) ← ગુણધર્મ
∴ y = 40°
હવે, y + z = 70° (∵ ઉપર સાબિત કર્યું.)
∴ 40° + 3 = 70°
∴ z = 70° – 40°
∴ z = 30°
આમ, x = 110°, y = 40° અને z = 30°

પ્રશ્ન 8. નીચેની આકૃતિ GUNS અને RUNS સમાંતરબાજુ ચતુષ્કોણ છે. x અને y શોધો. (લંબાઈ સેમીમાં છે.)
(i)

ઉત્તરઃ
□ GUNS એ સમાંતરબાજુ ચતુષ્કોણ છે.
∴ GS = NU અને SN = GU (∵ સામસામેની બાજુઓ)
∴ 3x = 18 અને 26 = 3y – 1
હવે, 3x = 18 ∴ x = 183
∴ x = 6
તથા 26 = 3y – 1
∴ 3y = 26 + 1
∴ 3y = 27
∴ y = 273
∴ y = 9
આમ, x = 6 સેમી અને y = 9 સેમી

(ii)

ઉત્તરઃ
□ RUNS એ સમાંતરબાજુ ચતુષ્કોણ છે.
□ RUNSના વિકર્ણો પરસ્પર દુભાગે છે.
∴y + 7 = 20
∴y = 20 – 7,
y = 13
અને x + y = 16માં y = 13 મૂકતાં,
x + 13 = 16
∴ x = 16 – 13
∴ x = 3
આમ, x = 3 સેમી અને y = 13 સેમી

પ્રશ્ન 9.

ઉપરની આકૃતિમાં RISK અને CLUE સમાંતરબાજુ ચતુષ્કોણ છે, તો x શોધો.
ઉત્તરઃ
અહીં □ RISK સમાંતરબાજુ ચતુષ્કોણ છે.
∴ m∠R+ m∠K = 180° (∵ પાસપાસેના બે ખૂણા પૂરકકોણ)
∴ m∠R + 120° = 180°
∴ m∠R = 180° – 120°
∴ m∠R = 60°
હવે ∠R અને ∠S એ સમાંતરબાજુ □ RISKના સામસામેના ખૂણા છે.
∴ m∠S = 60°
હવે □ CLUE એ સમાંતરબાજુ ચતુષ્કોણ છે.
∴ m∠E = m∠L = 90° (∵ સામસામેના ખૂણાનાં માપ સરખાં)
હવે, Δ ESQના ત્રણે ખૂણાનાં માપનો સરવાળો 180° થાય છે.
∴ m∠E + m∠S + x = 180°
∴ 70° + 60° + x = 180°
∴ 130° + x = 180°
∴ x = 180° – 130°
∴ x = 50°
આમ, x = 50°

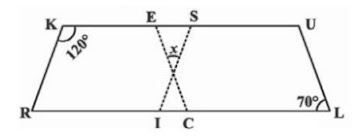
પ્રશ્ન 10. નીચેની આકૃતિ સમલંબ ચતુષ્કોણ કેવી રીતે છે, તે સમજાવો. કઈ બે બાજુ પરસ્પર સમાંતર છે?

ઉત્તરઃ
અહીં □ LMNKમાં m∠L + m∠M = 80° + 100° = 180°
એટલે કે □ LINKમાં ∠L અને ∠M એ પૂરકકોણો છે.
પણ આ NM¯¯¯¯¯¯¯¯∥KL¯¯¯¯¯¯¯ ને ML←→ છેદવાથી બનતા છેદિકાની એક જ બાજુના અંતઃકોણો છે.
∴ NM¯¯¯¯¯¯¯¯∥KL¯¯¯¯¯¯¯
□ NMNKમાં એક જ બાજુની જોડ NM¯¯¯¯¯¯¯¯∥KL¯¯¯¯¯¯¯ છે. તેથી આ ચતુષ્કોણ સમલંબ ચતુષ્કોણ છે.

પ્રશ્ન 11. આપેલી આકૃતિમાં જો AB¯¯¯¯¯¯¯¯∥DC¯¯¯¯¯¯¯¯¯ હોય, તો m∠C શોધો.

ઉત્તરઃ
□ ABCDમાં AB¯¯¯¯¯¯¯¯∥DC¯¯¯¯¯¯¯¯¯ છે.
∴ □ ABCD એ સમલંબ ચતુષ્કોણ છે.
અહીં AB¯¯¯¯¯¯¯¯∥DC¯¯¯¯¯¯¯¯¯ની છેદિકા BC←→ છે.
∴ m∠B + m∠C = 180°
(∵ છેદિકાની એક જ બાજુના અંતઃકોણો પૂરકકોણ હોય છે.)
∴ 120° + m∠C = 180°
∴ m∠C = 180° – 120° = 60°
આમ, m∠C = 60°

પ્રશ્ન 12. બાજુમાં આપેલ આકૃતિમાં, જો SP¯¯¯¯¯¯∥RQ¯¯¯¯¯¯¯¯ હોય, તો ∠P અને ∠Sનું માપ શોધો. (જો તમે m∠R શોધતા હોય, તો શું, m∠P શોધવાની અન્ય પદ્ધતિઓ હશે?)

ઉત્તરઃ
અહીં □ PQRSમાં SP¯¯¯¯¯¯∥RQ¯¯¯¯¯¯¯¯ છે.
∴ □ PQRS સમલંબ ચતુષ્કોણ છે.
SP¯¯¯¯¯¯∥RQ¯¯¯¯¯¯¯¯ની છેદિકા PQ←→ છે.
m∠P + m∠Q = 180° (∵ છેદિકાની એક જ બાજુના અંતઃકોણો)
∴ m∠P + 130° = 180°
∴ m∠P = 180° – 130°
∴ m∠P = 50°
હવે □ PQRSમાં ∠R કાટખૂણો છે.
SP¯¯¯¯¯¯∥RQ¯¯¯¯¯¯¯¯ અને તેને RS←→ છેદે છે.
∴ m∠S + m∠R = 180°
∴ m∠S + 90° = 180°
∴ m∠S + 180° – 90°
∴ m∠S = 90°

હા, ચતુષ્કોણના બધા ખૂણાઓનાં માપનો સરવાળો 360° થાય છે, તે પરથી પણ ∠P અને ∠R શોધી શકીએ.
∴ m∠P + m∠Q + m∠R + m∠S = 360°
∴ m∠P + 130° + 90° + 90° = 360°
∴ m∠P + 310° = 360°
∴ m∠P = 360° – 310°
∴ m∠P = 50

સ્વાધ્યાય 3.4

1. નીચેના વિધાનો સાચાં છે કે ખોટાં તે જણાવો.

પ્રશ્ન (a). દરેક લંબચોરસ ચોરસ છે.
ઉત્તરઃ ખોટું

પ્રશ્ન (b). દરેક સમબાજુ ચતુષ્કોણ સમાંતરબાજુ ચતુષ્કોણ છે.
ઉત્તરઃ ખરું

પ્રશ્ન (c). દરેક ચોરસ સમબાજુ ચતુષ્કોણ છે તેમજ લંબચોરસ પણ છે.
ઉત્તરઃ ખરું

પ્રશ્ન (d). દરેક ચોરસ સમાંતરબાજુ ચતુષ્કોણ નથી.
ઉત્તરઃ ખોટું

પ્રશ્ન (e). દરેક પતંગાકાર ચતુષ્કોણ સમબાજુ ચતુષ્કોણ છે.
ઉત્તરઃ ખોટું

પ્રશ્ન (f). દરેક સમબાજુ ચતુષ્કોણ પતંગાકાર ચતુષ્કોણ છે.
ઉત્તરઃ ખરું

પ્રશ્ન (g). દરેક સમાંતરબાજુ ચતુષ્કોણ સમલંબ ચતુષ્કોણ છે.
ઉત્તરઃ ખરું

પ્રશ્ન (h). દરેક ચોરસ સમલંબ ચતુષ્કોણ છે.
ઉત્તરઃ ખરું

2. એવા ચતુષ્કોણનાં નામ આપો કે જેમાં :

પ્રશ્ન (a). ચારેય બાજુની લંબાઈ સમાન હોય.
ઉત્તરઃ ચોરસ અને સમબાજુ ચતુષ્કોણની ચારેય બાજુઓની લંબાઈ સમાન હોય છે.

પ્રશ્ન (b). ચાર કાટખૂણા હોય. જવાબ:
ઉત્તરઃ ચોરસ અને લંબચોરસમાં ચારેય ખૂણા કાટખૂણા હોય છે.

3. કેવી રીતે એક ચોરસ એ

પ્રશ્ન (i). ચતુષ્કોણ
ઉત્તરઃ ચોરસને ચાર બાજુઓ છે તેથી તે ચતુષ્કોણ છે.

પ્રશ્ન (ii).સમાંતરબાજુ ચતુષ્કોણ
ઉત્તરઃ ચોરસની સામસામેની બાજુઓ સમાન છે તથા સમાંતર છે તેથી તે સમાંતરબાજુ ચતુષ્કોણ છે.

પ્રશ્ન (iii). સમબાજુ ચતુષ્કોણ
ઉત્તરઃ ચોરસની બધી બાજુઓ સમાન હોય છે તેથી તે સમબાજુ ચતુષ્કોણ છે.

પ્રશ્ન (iv). લંબચોરસ છે તે વિગતવાર સમજાવો.
ઉત્તરઃ ચોરસના બધા ખૂણા કાટખૂણા છે તેથી તે લંબચોરસ છે.

4. નીચે દર્શાવ્યા મુજબ વિકર્ણ ધરાવતાં ચતુષ્કોણનાં નામ આપો.

પ્રશ્ન (i). પરસ્પર દુભાગે
ઉત્તરઃ જેના વિકણ પરસ્પર દુભાગે છે તેવા ચતુષ્કોણ નીચે પ્રમાણે છે :

• સમાંતરબાજુ ચતુષ્કોણ
• લંબચોરસ
• ચોરસ
• સમબાજુ ચતુષ્કોણ

પ્રશ્ન (ii). પરસ્પરના લંબદ્વિભાજક હોય
ઉત્તરઃ જેના વિકર્ણો પરસ્પરના લંબદ્વિભાજક હોય તેવા ચતુષ્કોણ નીચે પ્રમાણે છે:

• ચોરસ
• સમબાજુ ચતુષ્કોણ

પ્રશ્ન (iii). સમાન હોય
ઉત્તરઃ જેના વિકણનાં માપ સમાન છે તેવા ચતુષ્કોણ નીચે પ્રમાણે છે :

• ચોરસ
• લંબચોરસ

5. લંબચોરસ એક બહિર્મુખ ચતુષ્કોણ છે, સમજાવો.
ઉત્તરઃ

• લંબચોરસમાં દરેક ખૂણાનું માપ 180° કરતાં ઓછું છે.
• બંને વિકણ લંબચોરસના અંદરના જ ભાગમાં હોય છે. તેથી લંબચોરસ એ બહિર્મુખ ચતુષ્કોણ છે.

6. કાટકોણ ત્રિકોણ ABCમાં કાટખૂણાની સામેની બાજુનું મધ્યબિંદુ O છે. શિરોબિંદુઓ A, B અને Cથી બિંદુ O કેવી રીતે સમાન અંતરે આવે છે તે સમજાવો. (અહીં તૂટક રેખાઓ તમારી સહાયતા માટે દોરેલ છે.)

ઉત્તરઃ
આકૃતિમાં BO−→− ને D સુધી લંબાવો જેથી BO = OD થાય.
હવે, CD¯¯¯¯¯¯¯ અને AD¯¯¯¯¯¯¯¯ દોરો.
□ ABCD તૈયાર થયો.
□ ABCDમાં AC = OC (∵ આપેલું છે.)
તથા BO = OD (∵ રચના)
∴ □ ABCDમાં વિકણ પરસ્પર દુભાગે છે.
∴ □ ABCD સમાંતરબાજુ ચતુષ્કોણ છે જેમાં ∠B કાટખૂણો છે. (∵ આપેલ છે.)
∴ □ ABCD એ લંબચોરસ છે.
હવે, લંબચોરસના વિકર્ણોનાં માપ સરખાં હોય છે અને પરસ્પર દુભાગે છે.
∴ AC = BD તથા AO = OC = BO = OD
આમ, O એ A, B અને Cથી સરખા અંતરે છે.