CHAPTER 4 - પ્રાયોગિક ભૂમિતિ

સ્વાધ્યાય 4.1

1. નીચેના ચતુષ્કોણની રચના કરોઃ

પ્રશ્ન (i). ચતુષ્કોણ ABCD
AB = 4.5 સેમી,
BC = 5.5 સેમી,
CD = 4 સેમી,
AD = 6 સેમી,
AC = 7 સેમી.

ઉત્તરઃ
રચનાના મુદ્દા (રચનાનાં સોપાન):

• 4.5 સેમી લંબાઈનો રેખાખંડ AB દોરો.
• પરિકર વડે A કેન્દ્ર અને 7 સેમી ત્રિજ્યા લઈ એક ચાપ દોરો.
• પરિકર વડે B કેન્દ્ર અને 5.5 સેમી ત્રિજ્યા લઈ અગાઉના ચાપને છેદતો ચાપ દોરો. બંને ચાપના છેદબિંદુને C કહો.
• પરિકર વડે A કેન્દ્ર અને 6 સેમી ત્રિજ્યા લઈ એક ચાપ દોરો.
• પરિકર વડે C કેન્દ્ર અને 4 સેમી ત્રિજ્યા લઈ અગાઉના ચાપને છેદતો ચાપ દોરો. બંને ચાપના છેદબિંદુને D કહો.
• BC¯¯¯¯¯¯¯,CD¯¯¯¯¯¯¯,AD¯¯¯¯¯¯¯¯ અને AC¯¯¯¯¯¯¯ દોરો.

આમ, □ ABCD એ માગ્યા મુજબનો ચતુષ્કોણ છે.

પ્રશ્ન (ii). ચતુષ્કોણ JUMP
JU = 3.5 સેમી,
UM = 4 સેમી,
MP = 5 સેમી,
PJ = 4.5 સેમી,
PU = 6.5 સેમી
ઉત્તરઃ

રચનાના મુદ્દા :

• 3.5 સેમી લંબાઈનો રેખાખંડ JU દોરો.
• પરિકર વડે J કેન્દ્ર અને 4.5 સેમી ત્રિજ્યાનો એક ચાપ દોરો.
• પરિકર વડે ઇ કેન્દ્ર અને 6.5 સેમી ત્રિજ્યાનો ચાપ દોરો જે અગાઉના ચાપને છે. બંને ચાપના છેદબિંદુને P કહો.
• પરિકર વડે ઇ કેન્દ્ર અને 4 સેમી ત્રિજ્યાનો એક ચાપ દોરો.
• પરિકર વડે ? કેન્દ્ર અને 5 સેમી ત્રિજ્યાનો ચાપ દોરો જે અગાઉના ચાપને છે. બંને ચાપના છેદબિંદુને M કહો.
• JP¯¯¯¯¯¯,UM¯¯¯¯¯¯¯¯,MP¯¯¯¯¯¯¯¯ અને UP¯¯¯¯¯¯¯ દોરો.

આમ, □ JUMP એ માગ્યા મુજબનો ચતુષ્કોણ છે.

પ્રશ્ન (iii). સમાંતરબાજુ ચતુષ્કોણ MORE
OR = 6 સેમી,
RE = 4.5 સેમી,
EO = 7.5 સેમી
ઉત્તરઃ

સમજૂતીઃ
□ MORE એ સમાંતરબાજુ ચતુષ્કોણ છે. તેની સામસામેની બાજુઓની લંબાઈ સરખી હોય.
∴RE = MO = 4.5 સેમી; OR = ME = 6 સેમી હોય.

રચનાના મુદ્દા :

• 4.5 સેમી લંબાઈનો રેખાખંડ MO દોરો.
• M કેન્દ્ર અને 6 સેમી ત્રિજ્યા લઈ એક ચાપ દોરો.
• O કેન્દ્ર અને 7.5 સેમી ત્રિજ્યા લઈ ચાપ દોરો જે અગાઉના ચાપને છેદે. બંને ચાપના છેદબિંદુને E કહો.
• O કેન્દ્ર અને 6 સેમી ત્રિજ્યાનો એક ચાપ દોરો.
• E કેન્દ્ર અને 4.5 સેમી ત્રિજ્યાનો ચાપ દોરો જે અગાઉના ચાપને છેદે. બંને ચાપના છેદબિંદુને R કહો.
• ME¯¯¯¯¯¯¯¯,OR¯¯¯¯¯¯¯¯,RE¯¯¯¯¯¯¯ અને OE¯¯¯¯¯¯¯ દોરો.

આમ, □ MORE એ માગ્યા મુજબનો ચતુષ્કોણ છે.

પ્રશ્ન (iv). સમબાજુ ચતુષ્કોણ BEST
BE = 4.5 સેમી,
ET = 6 સેમી
ઉત્તરઃ

સમજૂતીઃ □ BEST એ સમબાજુ ચતુષ્કોણ છે. તેની ચારે બાજુઓની લંબાઈ સરખી હોય.
BE = 4.5 સેમી ∴ ES = ST = TB = 4.5 સેમી તથા
ET = 6 સેમી છે.

રચનાના મુદ્દાઃ

• 4.5 સેમી લંબાઈનો રેખાખંડ BE દોરો.
• B કેન્દ્ર અને 4.5 સેમી ત્રિજ્યાનો એક ચાપ દોરો.
• E કેન્દ્ર અને 6 સેમી ત્રિજ્યાનો ચાપ દોરો જે અગાઉના ચાપને છેદે. બંને ચાપના છેદબિંદુને T કહો.
• E કેન્દ્ર અને 4.5 સેમી ત્રિજ્યાનો એક ચાપ દોરો.
• કેન્દ્ર અને 4.5 સેમી ત્રિજ્યાનો ચાપ દોરો જે અગાઉના ચાપને છે. બંને ચાપના છેદબિંદુને s કહો.
• BT¯¯¯¯¯¯¯,ES¯¯¯¯¯¯,ST¯¯¯¯¯¯ અને ET¯¯¯¯¯¯¯ દોરો.

આમ, □ BEST એ માગ્યા મુજબનો ચતુષ્કોણ છે.

સ્વાધ્યાય 4.2

1. નીચેના ચતુષ્કોણની રચના કરોઃ

પ્રશ્ન (i). ચતુષ્કોણ LIFT
LI = 4 સેમી,
IF = 3 સેમી,
TL = 2.5 સેમી,
LF = 4.5 સેમી,
IT = 4 સેમી
ઉત્તરઃ

રચનાના મુદ્દા:

• 4 સેમી લંબાઈનો રેખાખંડ LI દોરો.
• L કેન્દ્ર અને 2.5 સેમી ત્રિજ્યા લઈ એક ચાપ દોરો.
• I કેન્દ્ર અને 4 સેમી ત્રિજ્યાનો ચાપ દોરો જે અગાઉના ચાપને છેદે. બંને ચાપના છેદબિંદુને T કહો.
• L કેન્દ્ર અને 4.5 સેમી ત્રિજ્યાનો એક ચાપ દોરો.
• I કેન્દ્ર અને 3 સેમી ત્રિજ્યાનો ચાપ દોરો જે અગાઉના ચાપને છેદે. બને ચાપના છેદબિંદુને F કહો.
• LT¯¯¯¯¯¯¯,IF¯¯¯¯¯,FT¯¯¯¯¯¯¯,LF¯¯¯¯¯¯ અને IT¯¯¯¯¯¯ દોરો.

આમ, □ LIFT એ માગ્યા મુજબનો ચતુષ્કોણ છે.

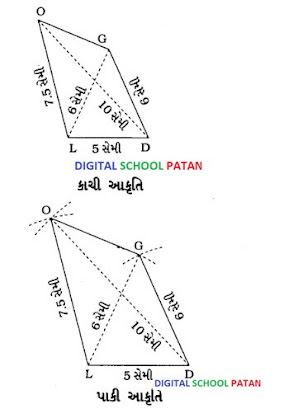
પ્રશ્ન (ii). ચતુષ્કોણ GOLD
OL = 7.5 સેમી,
GL = 6 સેમી,
GD = 6 સેમી,
ID = 5 સેમી,
OD = 10 સેમી
ઉત્તરઃ

રચનાના મુદ્દા:

• 5 સેમી લંબાઈનો રેખાખંડ LD દોરો.
• L કેન્દ્ર અને 7.5 સેમી ત્રિજ્યાનો એક ચાપ દોરો.
• D કેન્દ્ર અને 10 સેમી ત્રિજ્યાનો ચાપ દોરો જે અગાઉના ચાપને છેદે. બંને ચાપના છેદબિંદુને તે કહો.
• L કેન્દ્ર અને 6 સેમી ત્રિજ્યાનો એક ચાપ દોરો.
• D કેન્દ્ર અને 6 સેમી ત્રિજ્યાનો ચાપ દોરો જે અગાઉના ચાપને G બિંદુમાં છેદે.
• LO¯¯¯¯¯¯¯,GO¯¯¯¯¯¯¯¯,DG¯¯¯¯¯¯¯¯,LG¯¯¯¯¯¯¯ અને DO¯¯¯¯¯¯¯¯ દોરો.

આમ, □ GOLD એ માગ્યા મુજબનો ચતુષ્કોણ છે.

પ્રશ્ન (iii). સમબાજુ ચતુષ્કોણ BEND
BN = 5.6 સેમી,
DE = 6.5 સેમી
ઉત્તરઃ

સમજૂતીઃ
સમબાજુ ચતુષ્કોણના વિકર્ણો પરસ્પર કાટખૂણે દુભાગે છે. અહીં
સમબાજુ ચતુષ્કોણ BENDના વિકર્ણો DE¯¯¯¯¯¯¯ અને BN¯¯¯¯¯¯¯ પરસ્પર કાટખૂણે A બિંદુએ દુભાંગે છે. BN = 5.6 સેમી છે. તેથી AN = 2.8 સેમી અને AB = 2.8 સેમી થાય. અહીં DE¯¯¯¯¯¯¯નો લંબદ્વિભાજક દોરીને ચતુષ્કોણ BEND રચી શકાશે.

રચનાના મુદ્દા :

• 6.5 સેમી લંબાઈનો રેખાખંડ DE દોરો.
• DE¯¯¯¯¯¯¯નો લંબદ્વિભાજક XY←→ દોરો. XY←→ અને DE←→ના છેદબિંદુને A કહો.
• A કેન્દ્ર અને ત્રિજ્યા = 5.6 × 12 = 2.8 સેમી લઈ XY←→ને છેદતા બે ચાપ દોરો. આ બંને ચાપ XY←→ને છેદે ત્યાં અનુક્રમે B અને N કહો.
• DN¯¯¯¯¯¯¯¯,EN¯¯¯¯¯¯¯,EB¯¯¯¯¯¯¯ અને DB¯¯¯¯¯¯¯ દોરો.

આમ, □ BEND એ માગ્યા મુજબનો સમબાજુ ચતુષ્કોણ છે.

[નોંધ: ખૂણાનું માપ બે રીતે દર્શાવી શકાય તેવું આ પાઠ્યપુસ્તકમાં સૂચવ્યું છે. દા. ત., m∠A = 50° અથવા ∠A = 50°]

સ્વાધ્યાય 4.3

1. નીચેના ચતુષ્કોણની રચના કરોઃ

(1) ચતુષ્કોણ MORE
MO = 6 સેમી,
OR = 4.5 સેમી,
∠M = 60°,
∠M = 105°,
∠R = 105°

ઉત્તરઃ

રચનાના મુદ્દા :

• 6 સેમી લંબાઈનો રેખાખંડ MO દોરો.
• M બિંદુએ MA−→− એવું રચો કે જેથી m ∠ OMA = 60° થાય.
• O બિંદુએ OB−→− એવું રચો કે જેથી m ∠ MOB = 105° થાય.
• OB−→− ઉપર O કેન્દ્ર લઈ 4.5 સેમીનો ચાપ દોરો જે OB−→−ને છેદે, તેને R નામ આપો.
• R બિંદુએ RC−→− એવું રચો કે જેથી m ∠ ORC = 105° થાય.
• RC−→− અને MA−→−ના છેદબિંદુને E કહો.

આમ, □ MORE એ માગ્યા મુજબનો ચતુષ્કોણ છે.

(2). ચતુષ્કોણ PLAN
PL = 4 સેમી,
LA = 6.5 સેમી,
∠P = 90°,
∠A = 110°,
∠N = 85°
ઉત્તરઃ

સમજૂતીઃ □ PLANમાં m∠P = 90°, m∠A = 110° અને m∠N = 85°
∴ m∠L = 360° – (m∠P + m∠A + m∠N)
= 360° – (90° + 110° + 85°)
= 360° – 285°
= 75°

રચનાના મુદ્દાઃ

• 6.5 સેમી લંબાઈનો રેખાખંડ AL દોરો.
• AL¯¯¯¯¯¯¯ના A બિંદુએ 110નો ખૂણો બનાવતું AX−→− રચો. (કોણમાપકનો ઉપયોગ કરો.)
• AL¯¯¯¯¯¯¯ના બિંદુએ 75નો ખૂણો બનાવતું AY−→− રચો. (કોણમાપકનો ઉપયોગ કરો.)
• Lને કેન્દ્ર લઈ 4 સેમીનો ચાપ LY−→ ઉપર દોરો. છેદબિંદુને P કહો.
• P બિંદુએ 90°નો ખૂણો બનાવતું PZ−→ રચો.
• AX−→− અને PZ−→ના છેદબિંદુને N કહો.

આમ, □ PLAN એ માગ્યા મુજબનો ચતુષ્કોણ છે.
[નોંધઃ પાઠ્યપુસ્તકની રકમમાં ∠A = 10° છે તે ભૂલ છે તે સુધારી છે.]

(3). સમાંતરબાજુ ચતુષ્કોણ HEAR
HE = 5 સેમી,
EA = 6 સેમી,
∠R = 85°

ઉત્તરઃ

સમજૂતીઃ □ HEAR એ સમાંતરબાજુ ચતુષ્કોણ છે. સમાંતરબાજુ ચતુષ્કોણની સામસામેની બાજુઓ સરખી હોય છે.
HE = 5 સેમી ∴ AR = 5 સેમી; EA = 6 સેમી
∴ HR = 6 સેમી
સમાંતરબાજુ ચતુષ્કોણના પાસપાસેના ખૂણા પૂરકકોણ હોય છે.
m∠R = 85° ∴ m∠H = 180° – 85° = 95°
સમાંતરબાજુ ચતુષ્કોણના સામસામેના ખૂણા સરખા હોય છે.
m∠R = 85° ∴ m∠E = 85°

રચનાના મુદ્દા:

• 5 સેમી લંબાઈનો રેખાખંડ HE દોરો.
• HE¯¯¯¯¯¯¯ના H બિંદુએ 95નો ખૂણો બનાવતું HX−→− રચો. (કોણમાપકનો ઉપયોગ કરો.)
• H કેન્દ્ર લઈ 6 સેમી ત્રિજ્યાનો HX−→−ને છેદતો ચાપ દોરો. છેદબિંદુને R કહો.
• HE¯¯¯¯¯¯¯ના E બિંદુએ 85નો ખૂણો બનાવતું EY−→ રચો. (કોણમાપકનો ઉપયોગ કરો.)
• E કેન્દ્ર લઈ 6 સેમી ત્રિજ્યાનો EY−→ને છેદતો ચાપ દોરો. છેદબિંદુને A કહો.
• AR¯¯¯¯¯¯¯ દોરો.

□ HEAR એ માગ્યા મુજબનો સમાંતરબાજુ ચતુષ્કોણ છે.

(4). લંબચોરસ OKAY
OK = સેમી,
KA = 3 સેમી

ઉત્તરઃ

સમજૂતીઃ અહીં □ OKAY એ લંબચોરસ છે. લંબચોરસની સામસામેની બાજુઓ સરખી હોય છે.
∴ OK = 7 સેમી ∴ AY = 7 સેમી
અને KA = 5 સેમી ∴ OY = 5 સેમી
વળી લંબચોરસના બધા ખૂણા કાટખૂણા હોય છે.
∴ m∠O = m∠K = m∠A = m∠Y = 90°

રચનાના મુદ્દા :

• 7 સેમી લંબાઈનો રેખાખંડ OK દોરો.
• OK¯¯¯¯¯¯¯¯ના O બિંદુએ 90°નો ખૂણો બનાવતું OM−→− રચો.
• O કેન્દ્ર લઈ 5 સેમી ત્રિજ્યાનો OM−→−ને છેદતો ચાપ દોરો. છેદબિંદુને Y કહો.
• OK¯¯¯¯¯¯¯¯ના K બિંદુએ 90°નો ખૂણો બનાવતું KN−→− રચો.
• K કેન્દ્ર લઈ 5 સેમી ત્રિજ્યાનો KN−→−ને છેદતો ચાપ દોરો. છેદબિંદુને A કહો.
• AY¯¯¯¯¯¯¯¯ દોરો.

□ OKAY એ માગ્યા મુજબનો લંબચોરસ છે.

સ્વાધ્યાય 4.4

1. નીચેના ચતુષ્કોણની રચના કરોઃ

 (i). ચતુષ્કોણ DEAR
DE = 4 સેમી,
EA = 5 સેમી,
AR = 4.5 સેમી,
∠E = 60°,
∠A = 90°

ઉત્તરઃ

રચનાના મુદ્દાઃ

• 4 સેમી લંબાઈનો રેખાખંડ DE દોરો.
• DE¯¯¯¯¯¯¯ના E બિંદુએ 60° નો ખૂણો બનાવતું EM−→− રચો.
• E કેન્દ્ર લઈ 5 સેમી ત્રિજ્યાનો EM−→−ને છેદતો ચાપ દોરો. છેદબિંદુને A કહો.
• EA¯¯¯¯¯¯¯ પર A બિંદુએ 90°નો ખૂણો બનાવતું AN−→− દોરો.
• A કેન્દ્ર લઈ 4.5 સેમી ત્રિજ્યાનો AN−→−ને છેદતો ચાપ દોરો. છેદબિંદુને R કહો.
• DR¯¯¯¯¯¯¯¯ દોરો.

□ DEAR એ માગ્યા મુજબનો ચતુષ્કોણ છે.

 (ii). ચતુષ્કોણ TRUE
TR = 3.5 સેમી,
RU = 3 સેમી,
UE = 4 સેમી,
∠R = 75°,
∠U = 120°

ઉત્તરઃ

રચનાના મુદ્દા :

• 3.5 સેમી લંબાઈનો TR¯¯¯¯¯¯¯ દોરો.
• TR¯¯¯¯¯¯¯ના R બિંદુએ 75°ના માપનો ખૂણો બનાવતું RM−→− દોરો.
• R કેન્દ્ર લઈ 3 સેમી ત્રિજ્યાનો RM−→−ને છેદતો ચાપ દોરો. છેદબિંદુને U કહો.
• RU¯¯¯¯¯¯¯ના U બિંદુએ 120°નો ખૂણો બનાવતું UN−→− દોરો. (કોણમાપકનો ઉપયોગ કરો.)
• U કેન્દ્ર લઈ 4 સેમી ત્રિજ્યાનો UN−→−ને છેદતો ચાપ દોરો. છેદબિંદુને E કહો.
• ET¯¯¯¯¯¯¯ દોરો.

આમ, □ TRUE એ માગ્યા મુજબનો ચતુષ્કોણ છે.

સ્વાધ્યાય 4.5

નીચેની રચના કરોઃ

(1) . RE = 5.1 સેમી ધરાવતો ચોરસ READ રચો.

ઉત્તરઃ

રચનાના મુદ્દા:

• 5.1 સેમી લંબાઈનો રેખાખંડ RE દોરો.
• RE¯¯¯¯¯¯¯ના E બિંદુએ 90° નો ખૂણો બનાવતું EM−→− રચો.
• E કેન્દ્ર લઈ 5.1 સેમી ત્રિજ્યાનો ચાપ દોરો જે EM−→−ને છેદે, છેદબિંદુને A કહો.
• R કેન્દ્ર લઈ 5.1 સેમી ત્રિજ્યાનો ચાપ દોરો.
• A કેન્દ્ર લઈ 5.1 સેમી ત્રિજ્યાનો ચાપ દોરો જે અગાઉના ચાપને છેદે. છેદબિંદુને D કહો.
• RD¯¯¯¯¯¯¯¯ અને AD¯¯¯¯¯¯¯¯ દોરો.

□ READ એ માગ્યા મુજબનો ચોરસ છે.

 (2). જેના વિકર્ણોની લંબાઈ 5.2 સેમી અને 6.4 સેમી હોય તેવો સમબાજ ચતુષ્કોણ રચો.

ઉત્તરઃ

સમજૂતી :
સમબાજુ ચતુષ્કોણના વિકર્ણો પરસ્પર કાટખૂણે દુભાગે છે. અહીં સમબાજુ ચતુષ્કોણ XYZWમાં YW = 6.4 સેમી
∴ OW = OY = 3.2 સેમી થાય.

રચનાના મુદ્દા:

• 5.2 સેમી લંબાઈનો રેખાખંડ XZ દોરો.
• XZ¯¯¯¯¯¯¯નો લંબદ્વિભાજક AB←→ દોરો જે XZ¯¯¯¯¯¯¯ જે બિંદુમાં છેદે તેને 0 નામ આપો.
• O કેન્દ્ર અને 3.2 સેમી ત્રિજ્યાનો ચાપ દોરો જે AB←→ને ઉપરના ભાગમાં છે. છેદબિંદુને W નામ આપો.
• O કેન્દ્ર અને 3.2 સેમી ત્રિજ્યાનો બીજો ચાપ દોરો જે AB←→ને નીચેના ભાગમાં છેદે. છેદબિંદુને Y નામ આપો.
• XY¯¯¯¯¯¯¯¯,YZ¯¯¯¯¯¯¯,ZW¯¯¯¯¯¯¯¯ અને XW¯¯¯¯¯¯¯¯¯ દોરો.

□ XYZW એ માગ્યા મુજબનો સમબાજુ ચતુષ્કોણ છે.

(3). એવા લંબચોરસની રચના કરો કે જેની પાસપાસેની બાજુઓની લંબાઈ 5 સેમી અને 4 સેમી હોય.

ઉત્તરઃ

(નોંધઃ લંબચોરસના બધા ખૂણા કાટખૂણા છે તેનો ઉપયોગ કરીશું.)

રચનાના મુદ્દા:

• 5 સેમી લંબાઈનો રેખાખંડ AB દોરો.
• AB¯¯¯¯¯¯¯ના A બિંદુએ 90°નો ખૂણો બનાવતું AX−→− રચો.
• A કેન્દ્ર લઈ 4 સેમી ત્રિજ્યાનો ચાપ દોરો જે AX−→−ને જ્યાં છેદે તેને D નામ આપો.
• B કેન્દ્ર લઈ 4 સેમી ત્રિજ્યાનો એક ચાપ દોરો.
• D કેન્દ્ર લઈ 5 સેમી ત્રિજ્યાનો ચાપ દોરો જે અગાઉના ચાપને છેદે. છેદબિંદુને C કહો.
• BC¯¯¯¯¯¯¯ અને CD¯¯¯¯¯¯¯ દોરો.

□ ABCD એ માગ્યા મુજબની લંબચોરસ છે.

4. સમાંતરબાજુ ચતુષ્કોણ OKAY રચો જ્યાં OK = 5.5 સેમી, KA = 4.2 સેમી હોય, શું આ અનન્ય છે?

ઉત્તરઃ

આપેલાં માપ પૂરતાં નથી. તેથી સમાંતરબાજુ ચતુષ્કોણ દોરી ન શકાય.
ધારો કે ∠O = 60° હોય, તો OK = 5.5 સેમી અને KA = 4.2 સેમી માપ પરથી સમાંતરબાજુ ચતુષ્કોણ રચી શકાય.
આપેલાં માપ જ હોય તેવા ઘણા બધા સમાંતરબાજુ ચતુષ્કોણ હોઈ શકે જેમાં ખૂણાનાં માપ જુદાં જુદાં હોય. તેથી આ સમાંતરબાજુ ચતુષ્કોણ અનન્ય નથી.